Conoscopy of Biaxial Minerals (1).

                Introduction.

                    The biaxial minerals are  members of the lower symmetry systems: orthorhombic, monoclinic and triclinic.  Their optical indicatrix has no circular symmetry anymore but is a general ellipsoid with three principal axes (a, b and g) which are the principal indices of refraction of the considered mineral. a  is the smaller index, g is the larger. Such an ellipsoid, has two circular sections with indices equal to b. The lines perpendicular to these circular sections are called optic axes, so biaxial crystals have two optic axes. The indices a and g are in the same plane as the optic axes and they bisect the optic axes angles.  The index b is perpendicular to the optic plane. Figure 1 shows a section of the biaxial indicatrix, the index b is perpendicular to the plane of the figure.  An optical sign can also be defined for those crystals: a positive crystal has its large index g as acute bisectrix of  the optic axes angle like in figure 1. For a negative crystal a is the acute bisectrix .

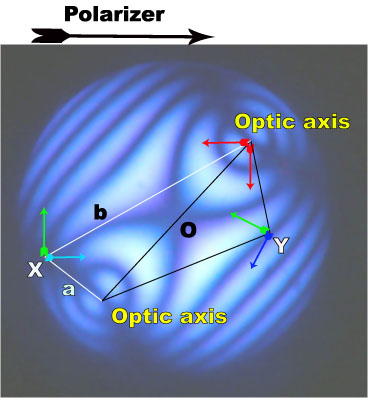
                    The same geometrical construction can be made to view the conoscopic image structure of a biaxial crystal perpendicular to the acute bisectrix as we deed for uniaxial crystals. In figure 1, main features of such an image are presented. To get a three dimensional picture, the conoscopic plane should be rotated by 90° around an horizontal axis. The poles of both optic axes appear in the figure with a birefringence equal to zero because both indices are b (cyclic section), they are thus always dark. At the center of the figure, the indices are a and b . Between the poles of the optic axes and the center of the figure, the indices parallel to the optic planes have values between a and b as can be seen on the indicatrix figure because such points in the conoscopic figure correspond to sections situated between the circular section and the section containing a (marked by the red line in the figure). For the points beyond the poles of the optic axes, the indices in the optic plane are greater then b and are called g' (sections between cyclic section and g ). The indices on this line being parallel to polarizer and analyzer belong to the isogyres and are thus situated on a dark line. 

                    Deduction of the orientation of refraction indices in other places of the figure is a little bit more complicated then explained for uniaxial crystals. The approximate solution is coming from the Biot-Fresnel law: draw the lines connecting the optic axes to the point of interest in the conoscopic figure. The bisectrix of these two lines determines the direction of one index in that position, the second index being perpendicular to the first one. Two examples of such a construction are given in  figure 1. At point Y the index g' is the bisector of lines c and d joining Y to the poles of the optic axes. The other index is perpendicular to g' and equal to a because the section in the indicatrix normal to point Y contains main index a. The same is true for all the points of the vertical line passing through Y. These two indices are parallel to polarizer and analyzer and thus belong to the isogyres.  The second example is given by point X, where the indices are bisector of lines a and b joining X to the poles of the optic axes. In that case, the direction of indices are no more colinear to the crossed polars so the interference colors could be seen.

                    For a crystal with its optic plane parallel to polarizer or analyzer, the isogyres are an asymmetric cross with a wider dark line normal to the optic plane. The orientation of indices changes slower on the vertical line between optic axes than in the region around optic axes as can be seen by experimenting with the Biot-Fresnel construction. This explain why the isogyres are  thinner close to the poles of the optic axes, particularly if the birefringence and thickness of the crystal plate are high.

                    The isochromes curves have also a more complicated shape as compared to the uniaxial conoscopy. For high birefringence and thickness, some of them resemble circles and ellipses around the optic axis. With the Biot-Fresnel construction, it is easy to see that indices directions rotate around the pole of the optic axis in a region close to it. At some distances from the axes, the extinction curves have the shape of Bernouilli's lemniscates.

                     The rotation of the optic plane by 45° gives the image in figure 2. This image was obtained in monochromatic light at 467 nm. Two groups of dark curves can be seen on the figure. Point X belongs to the isogyres because the indices obtained as bisector of the aXb angle are parallel to polarizer and analyzer. If we repeat this geometric construction, we get the complete isogyres which are now hyperboles passing through the poles of the optic axes. Other dark points like Y have indices in any orientation. They are dark because their retardation is a multiple of the wavelength of the light and belong thus to the isochromes. 

 Next page          [Conoscopy main page]                [Home]